Skip to content

Lab 1.5. PID Control

Estimated time to complete this lab: 1 hour

Objectives

At the end of this self-learning lab, you should be able to:

  • perform a basic feedback control loop to control a motor's rotation speed

Feedback control

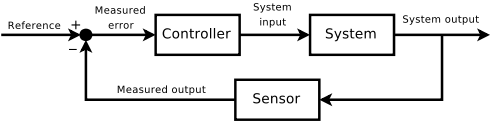
Feedback Control

From the previous lab, we only "hardcoded" a current to the motor. It keeps on accelerating until it reaches a "maximum RPM".

In order to control the speed of the motor to a set value, you can:

  1. Apply a certain current to the motor.
  2. Measure the speed of the motor and calculate the error, i.e. the difference between the desired speed and the actual speed.
  3. Recall that current is similar to acceleration. We should accelerate (increase current) if the speed is too low, vice versa. If the desired speed is close to the actual speed, the output current should be closer to zero. It may be more responsive if the adjustment is proportional to the error.
  4. Repeat 2 - 3.

A pseudocode that implements the above feedback loop is as follows:

// define constant kP
// user input velocity_setpoint (target)

loop {
    current_value = kP * (velocity_setpoint - velocity_feedback)

    send_current_command_to_motor(current_value)
}

This is called a negative feedback control. (The same as the one you learnt in secondary school biology) This method we have used is called proportional control.

Classwork 1.5.1

I have complete control

  • Write a code that can control the motor to rotate at around 1000 RPM.
  • Apply some resistance over the motor. How does the supplied current level changed? Can it maintain at 1000 RPM?

Please approach our team members after you have completed the task. In your training repository, save the code into a new file named cw-1-5-1.cpp. Commit and push the code. If you don't know how to use git/github, you can refer to the internal git tutorial here.

Extra: PID controller

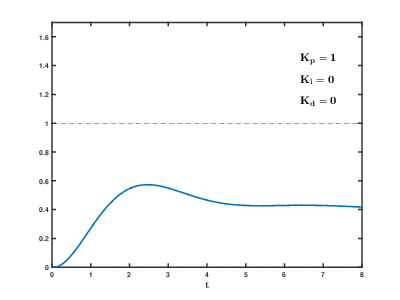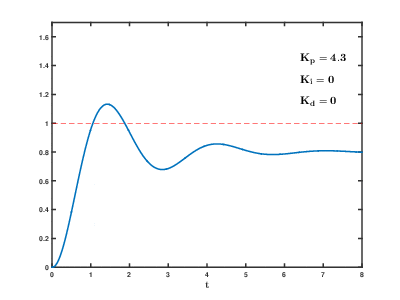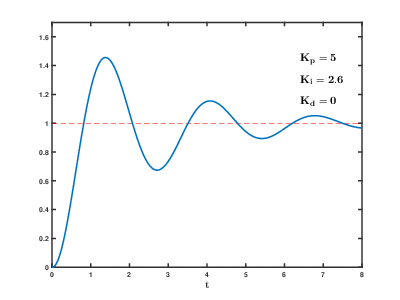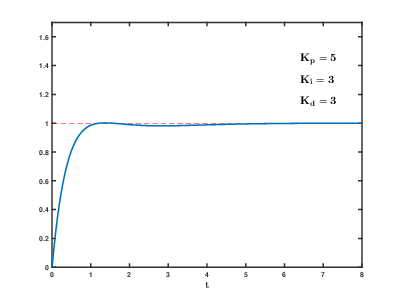
PID Compensation

Proportional control is a primitive control method and has many problems:

  • Slow response time
  • Unable to reach target
  • Overshoot and oscillate

There is another control method called PID control. It takes account of the proportional, integral, and derivative terms of the error.

You are strongly advised to watch these two videos, both by Northwestern Robotics professor Kevin Lynch:

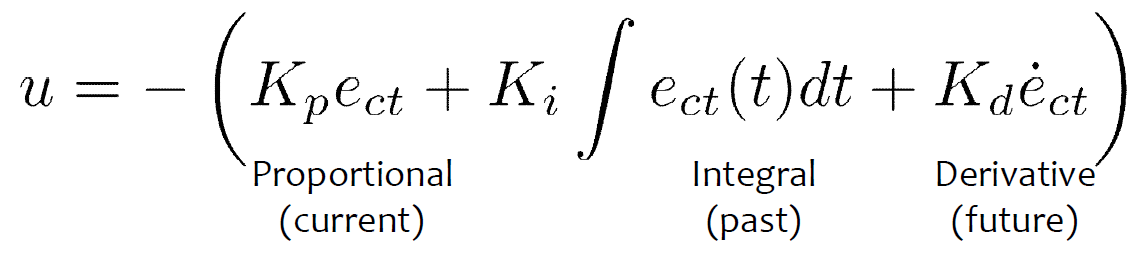
Feedback Control

The basic intuition is:

  • Proportional: get rid of the current error!
  • Integral – if I am accumulating error, try harder!
  • Derivative – if I am going to overshoot, slow down!

You should define the constants \(K_p, K_i, K_d\) by yourself. The \(e\) terms represent error and are meant to be measured from the system.

How to systematically find \(K_p, K_i, K_d\) is an active research topic. But a rule of thumb is:

  • You should increase \(K_p\) to the point until the feedback starts oscillating
  • If the feedback oscillates too much, increase \(K_d\) to "dampen" the system

Some variations of PID are P, PI, and PD.

  • P control means we set \(K_p > 0\) and \(K_i = K_d = 0\).
  • Likewise, PI control means we set \(K_p, K_i > 0\) and \(K_d = 0\).
  • Likewise, PD control means we set \(K_p, K_d > 0\) and \(K_i = 0\).
  • PID control means we set \(K_p, K_d, K_i > 0\).

P control (or sometimes PD) is sometimes sufficient for controlling motor speed. However, when controlling more complicated things (e.g. inverted pendulum) then full PID control may be needed.

External materials on PID